Dalam perjalanan panjang evolusi statistik, terdapat satu metode yang sering berfungsi sebagai pembuka pintu bagi sekian banyak analisis yang lebih kompleks: regresi linear sederhana. Bayangkan saat pertama kali manusia merenungkan tentang hubungan antara dua fenomena berbeda – seperti cuaca dan panen – di sanalah cikal bakal regresi pertama kali terbentuk. Seiring waktu berjalan, ahli statistik mulai merumuskan cara terstruktur untuk memprediksi hasil berdasar observasi masa lalu. Inilah asal usul dari regresi linear sederhana, sebuah alat analisis yang menawarkan jendela untuk memandang keterhubungan dua variabel.
Konsep Dasar Regresi Linear Sederhana
Regresi linear sederhana dapat didefinisikan sebagai metode statistik yang digunakan untuk memahami hubungan antara dua variabel kuantitatif. Satu variabel dianggap sebagai variabel independen atau prediktor, sementara yang lain sebagai variabel dependen atau hasil. Dalam analisis ini, tujuan utamanya adalah menemukan garis terbaik yang dapat memprediksi nilai variabel dependen berdasarkan nilai variabel independen. Begitu ditemukan, garis regresi ini tidak hanya membantu dalam memprediksi tetapi juga memberikan wawasan tentang bagaimana variabel-variabel tersebut berinteraksi satu sama lain.
Bayangkan seorang petani yang ingin memahami bagaimana curah hujan mempengaruhi hasil panennya. Dengan menggunakan analisis regresi linear sederhana, dia bisa membuat model untuk memprediksi hasil panen berdasarkan data curah hujan dari tahun-tahun sebelumnya. Demikian pula, seorang ekonom mungkin ingin mengetahui bagaimana perubahan suku bunga dapat mempengaruhi tingkat investasi di suatu negara. Regresi linear menjadi alat yang sangat penting untuk analisis semacam itu, memberikan cara yang ringkas untuk meringkas data dan membuat prediksi yang terinformasi. Pada intinya, regresi linear sederhana adalah tentang mencari garis yang dapat memberikan gambaran paling jelas tentang hubungan antara dua variabel.
Cara Kerja Analisis Regresi Linear Sederhana
Pertama, seorang peneliti harus mengumpulkan data dari dua variabel yang ingin dia teliti hubungan di antara keduanya. Setelah data terkumpul, langkah berikutnya adalah memetakan data ini pada bidang koordinat kartesius sehingga dapat divisualisasikan. Analisis regresi linear sederhana kemudian membantu dalam menetapkan garis terbaik, yang dikenal sebagai garis regresi, melalui titik-titik data tersebut.
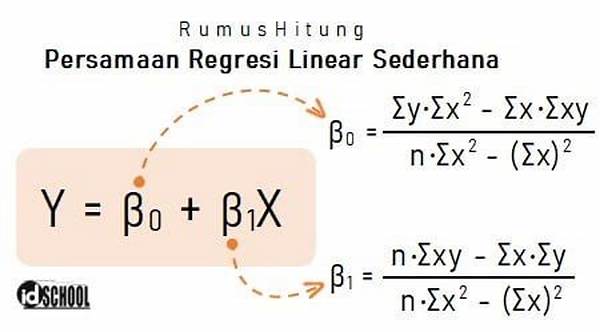
Kedua, dalam analisis regresi linear sederhana, terdapat asumsi bahwa hubungan antara kedua variabel adalah linear, yaitu dapat diwakili oleh sebuah garis lurus. Asumsi linearitas ini seringkali disederhanakan dalam model persamaan garis, yakni: Y = a + bX + e, dengan Y sebagai variabel dependen.
Ketiga, untuk mendapatkan persamaan garis regresi tersebut, metode kuadrat terkecil atau least squares method sering digunakan. Ini adalah teknik matematika yang berusaha meminimalkan jumlah kuadrat dari selisih (residual) antara nilai yang diamati dan yang diprediksi oleh model.
Keempat, setelah mendapatkan persamaan garis, peneliti bisa menganalisis makna dari koefisien regresi. Koefisien pada variabel independen menandakan perubahan rata-rata yang diharapkan pada variabel dependen untuk setiap unit perubahan pada variabel independen.
Kelima, pentingnya analisis regresi linear sederhana juga terletak pada kemampuannya untuk mengevaluasi kekuatan hubungan antara variabel. Melalui koefisien determinasi, yang sering kali diungkapkan dalam persentase, peneliti dapat mengukur konsistensi hubungan linear tersebut.
Asumsi dalam Analisis Regresi Linear Sederhana
Saat berbicara tentang analisis regresi linear sederhana, penting untuk memahami asumsi dasar yang mendasari model ini. Asumsi pertama yang perlu diperhatikan adalah bahwa hubungan antara variabel dependen dan independen bersifat linear. Ini berarti bahwa perubahan pada variabel independen akan menghasilkan perubahan secara proporsional pada variabel dependen. Jika hubungan ini tidak linear, model regresi linear sederhana mungkin tidak akan memberikan hasil yang akurat.
Selain itu, asumsi kedua adalah bahwa variabel independen bersifat bebas dari error pengukuran. Dalam konteks ini, kita menganggap bahwa pengukuran variabel independen dilakukan dengan alat ukur yang presisi tinggi sehingga error pengukuran bisa diabaikan. Asumsi ketiga berkaitan dengan homoskedastisitas, di mana variabilitas dari error atau residual adalah konstan di seluruh rentang variabel independen. Ini berarti distribusi error tidak menyempit atau melebar dengan nilai yang berubah dari variabel independen.
Ketika asumsi-asumsi ini terpenuhi, hasil regresi linear sederhana dapat dipercaya. Namun, kenyataan di lapangan sering kali menunjukkan sebaliknya. Dengan kondisi data yang sarat bias atau pengukuran yang kurang akurat, seorang peneliti harus sangat berhati-hati dalam menginterpretasikan hasil dari analisis regresi linear sederhana.
Penerapan dan Keunggulan Analisis Regresi Linear Sederhana
Penerapan analisis regresi linear sederhana dalam kehidupan sehari-hari tak terhitung banyaknya. Mulai dari sektor pertanian, ekonomi, hingga ilmu sains, model ini membantu memberikan gambaran yang lebih jelas terhadap hubungan antar variabel. Misalnya, pengusaha retail dapat menggunakan model ini untuk memproyeksikan penjualan berdasarkan tingkat pengeluaran pemasaran. Dalam bidang kesehatan, hubungan antara tekanan darah dan usia bisa dianalisis menggunakan regresi linear sederhana untuk tujuan penelitian klinis.
Selain itu, salah satu keunggulan utama dari analisis regresi linear sederhana adalah kesederhanaannya. Alat ini tidak memerlukan pemahaman mendalam mengenai matematika tingkat tinggi dan dapat diimplementasikan dengan mudah menggunakan perangkat lunak statistik seperti Excel atau SPSS. Penggunaan yang relatif mudah ini membuatnya menjadi pilihan yang tepat bagi banyak peneliti, terutama mereka yang baru memulai eksplorasi dalam analisis statistik.
Namun, meskipun sederhananya, model ini memiliki kelemahan dalam mengatasi kerumitan hubungan yang lebih kompleks antara variabel. Ketergantungan pada asumsi linearitas dapat mengakibatkan kesalahan dalam interpretasi ketika diterapkan pada data non-linear. Dengan menyadari kelebihan dan batasannya, analisis regresi linear sederhana tetap menjadi alat penting yang sering digunakan dalam penelitian ilmiah dan aplikasi praktis.
Tantangan dalam Menggunakan Analisis Regresi Linear Sederhana
Walaupun regresi linear sederhana adalah alat yang kuat, menggunakan model ini bukan tanpa tantangan. Tantangan pertama yang dihadapi peneliti adalah memastikan bahwa data yang digunakan sesuai dengan asumsi-asumsi dasar model. Misalnya, kesalahan dalam menentukan homoskedastisitas bisa mengakibatkan hasil yang bias. Oleh karena itu, sering kali peneliti harus menggunakan uji statistik tambahan untuk memeriksa validitas asumsi ini sebelum melangkah lebih jauh.
Tantangan kedua adalah dalam pemilihan variabel yang tepat. Memilih variabel independen yang tidak relevan atau menggunakan data yang tidak akurat dapat mengurangi keandalan hasil analisis regresi linear sederhana. Peneliti harus berhati-hati untuk memastikan bahwa variabel yang dipilih benar-benar memiliki hubungan teoritis yang kuat dengan variabel dependen, sehingga model yang dihasilkan tidak hanya secara statistik signifikan tetapi juga bermakna secara substantif.
Tantangan ketiga adalah dalam interpretasi hasil regresi. Sementara persamaan regresi dapat secara langsung memberikan nilai prediksi, memahami implikasi dari koefisien regresi dalam konteks yang lebih luas memerlukan keahlian dan analisis kritis lebih lanjut. Dengan demikian, meskipun tampaknya sederhana, analisis regresi linear sederhana memerlukan tingkat penerapan dan penilaian yang cermat untuk mendapatkan intisari serta manfaat maksimal dari data.
Kesimpulan
Analisis regresi linear sederhana adalah salah satu alat paling fundamental dalam statistik yang menawarkan pandangan awal tentang hubungan antara dua variabel. Meskipun sederhana, alat ini memberikan landasan yang kuat untuk memahami interaksi linear antara variabel-variabel yang diteliti. Mulai dari prediksi penjualan berdasarkan faktor demografis hingga mengukur dampak perubahan iklim terhadap produksi pangan, regresi linear memberikan kemampuan prediksi yang penting bagi peneliti dari berbagai disiplin ilmu.
Namun, untuk mendapatkan hasil maksimal dari analisis regresi linear sederhana, kepekaan terhadap asumsi-asumsi yang mendasari model ini adalah kunci. Melalui pemahaman yang baik tentang data dan konteks di mana data tersebut diaplikasikan, beragam tantangan yang muncul dapat diidentifikasi dan, jika perlu, diatasi dengan model yang lebih kompleks. Meski begitu, regresi linear sederhana tetap menjadi alat analisis yang terus digunakan karena kemampuannya memberikan gambaran yang nyata tentang hubungan variabel yang sederhana namun kritis.