Di sebuah kantor pusat kota yang hiruk-pikuk, seorang analis data muda merenung di depan layar komputernya. Data demi data menjuntai seperti lembaran teka-teki yang menanti untuk dipecahkan. Tugasnya adalah menyelami kedalaman angka dan menemukan pola yang tersembunyi di dalamnya. Hari itu, ia sedang dihadapkan dengan masalah yang menantang: analisis data menggunakan distribusi normal. Dalam perjalanannya mengenali pola ini, ia yakin bahwa distribusi normal, atau yang sering disebut sebagai distribusi Gaussian, adalah kunci dalam memahami kompleksitas data yang tampaknya acak.
Dasar-Dasar Distribusi Normal
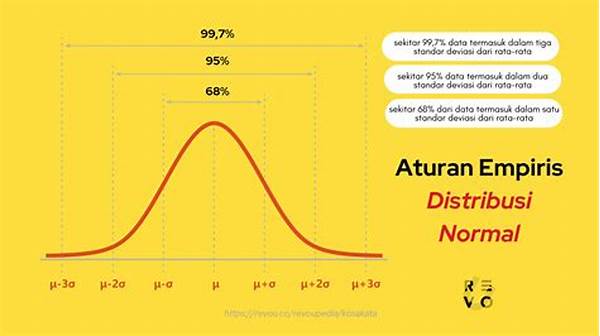
Distribusi normal adalah salah satu konsep utama dalam ilmu statistik. Dengan kurva lonceng simetri yang dimilikinya, distribusi ini menggambarkan bagaimana data terdistribusi secara alami di alam dan masyarakat. Sebagai contoh, tinggi badan manusia dan skor ujian sering memperlihatkan pola distribusi normal. Analis data muda itu memahami pentingnya distribusi normal karena ini memungkinkan prediksi dan asumsi yang lebih akurat. Saat ia menggali lebih dalam, ia menyadari bahwa distribusi normal menegaskan betapa sebagian besar data akan berkumpul di sekitar rata-rata. Dengan analisis data menggunakan distribusi normal, ia bisa menentukan dengan tepat mana data yang termasuk dalam anomali dan mana yang merupakan bagian dari pola biasa.
Ketika dia menerapkan distribusi normal pada dataset-nya, ia bisa melihat pola yang sebelumnya tersembunyi. Proses ini tidak hanya melibatkan perhitungan mean dan deviasi standar, tetapi juga memahami bentuk dan ukuran data tersebut. Keteraturan yang disajikan oleh distribusi normal memberi analis itu wawasan berharga tentang bagaimana dataset-nya berperilaku dalam kondisi normal. Melalui analisis data menggunakan distribusi normal, ia mampu menemukan titik-titik penting yang dapat menaikkan tingkat akurasi keputusan bisnis dan ilmiah tempatnya bekerja.
Menggunakan distribusi normal membutuhkan pemahaman yang mendalam tentang bagaimana data dapat diproses dan diinterpretasikan. Analis itu belajar bahwa tidak semua data mengikuti pola ini. Namun, untuk dataset yang sesuai, pemanfaatan distribusi normal mampu memberikan hasil yang memperkaya pemahaman. Ia mengamati bahwa analisis data menggunakan distribusi normal mempermudah identifikasi hubungan di antara data, sekaligus menguatkan keakuratan perkiraan dan prediksi yang dibuat terhadap dataset yang ditelaah.
Mengapa Distribusi Normal Penting?
Analisis data menggunakan distribusi normal adalah fondasi penting dalam statistik yang memudahkan penyusunan hipotesis dan pengujian asumsi. Distribusi normal memfasilitasi prediksi karena sebagian besar variasi mengikuti pola yang dikenali.
Dalam kehidupan sehari-hari, banyak situasi yang sesuai dengan distribusi normal, seperti tinggi rata-rata dan IQ populasi. Dengan menggunakan distribusi ini, analis memperoleh pemahaman mendalam tentang sifat dataset yang dihadapi. Analisis data menggunakan distribusi normal memungkinkan pembuatan model prediktif yang lebih akurat.
Selain itu, distribusi normal membantu dalam pengujian hipotesis yang merupakan bagian esensial dalam penelitian ilmiah. Sebagai dasar, distribusi ini menawarkan metode yang efisien untuk menganalisis dan menyimpulkan data. Dalam banyak kasus, distribusi normal menjadi jangkar bagi kajian empiris yang memerlukan pengujian signifikan.
Penerapan Distribusi Normal dalam Analisis Data
Ketika seorang analis mulai menerapkan analisis data menggunakan distribusi normal pada proyeknya, dia menemukan pencerahan melalui data yang sebelumnya dianggap acak dan tidak teratur. Dalam lingkungan bisnis, distribusi normal diterapkan pada analisis resiko untuk meramalkan fluktuasi pasar dan memahami potensi kerugian dan keuntungan.
Penerapan distribusi normal juga sangat relevan dalam dunia medis, di mana pola distribusi ini berguna untuk menginterpretasikan hasil tes laboratorium. Setiap hasil tes mungkin mengikuti distribusi normal, yang memudahkan para dokter dalam menetapkan diagnosis dan menentukan tindakan medis yang tepat.
Dalam bidang pendidikan, distribusi normal mempermudah evaluasi kinerja siswa di seluruh batasan distribusi. Rata-rata dan kelainan standar sering digunakan untuk menilai seberapa jauh seorang siswa atau kelompok siswa berada dari performa umum. Analisis data menggunakan distribusi normal membantu pendidikan lebih memahami standar pengajaran dan mengidentifikasi area yang butuh perbaikan.
Menyikapi Tantangan dalam Distribusi Normal
Menghadapi dataset yang besar dan kompleks, ada kalanya distribusi normal tidak dapat langsung diterapkan karena beberapa data mungkin tidak mengikuti pola ini. Analis harus mampu mengenali kapan distribusi normal relevan dan bermanfaat. Pemahaman tentang bagaimana mengadopsi dan menyesuaikan model distribusi normal ketika menghadapi outliers menjadi krusial dalam pekerjaan analis.
Dalam banyak proyek analisis data, distribusi normal berperan sebagai titik awal yang penting untuk memahami perilaku umum data. Namun, para analis juga dihadapkan dengan kebutuhan untuk mempertimbangkan distribusi lain yang mungkin lebih sesuai tergantung pada kebutuhan dan karakteristik dataset yang dianalisis.
Analisis data menggunakan distribusi normal bukanlah satu-satunya metode yang dipertimbangkan, tetapi ini adalah fondasi kuat yang memfasilitasi pengujian dan prediksi model lebih lanjut. Para analis harus bijak menyesuaikan pendekatan dan alat sesuai dengan situasi nyata yang dihadapi dalam proyek mereka.
Studi Kasus Distribusi Normal
Suatu hari, seorang analis data menerapkan distribusi normal untuk mengevaluasi tren penjualan di sebuah perusahaan retail besar. Dengan data penjualan bulanan selama 5 tahun terakhir, dia mencoba memprediksi periode puncak dan rendah permintaan.
Melalui analisis data menggunakan distribusi normal, dia dapat lebih memahami fluktuasi penjualan dengan perhatian khusus pada periode di mana data menyimpang dari normalitas. Temuannya menunjukkan pola konsisten yang memungkinkan perusahaan menyiapkan inventori dengan lebih baik. Analis data itu menyimpulkan bahwa dengan memahami pola distribusi, aktivitas bisnis lebih terkelola dan efisien.
Dalam skenario lain, seorang analis menerapkan distribusi normal untuk menentukan pola pertumbuhan penduduk di kota metropolitan. Data sensus yang diolah menunjukkan distribusi yang mendekati normal, membantu pemerintah dalam merencanakan infrastruktur yang lebih baik dan layanan publik yang efisien kepada masyarakat.
Kesimpulan Pemanfaatan Distribusi Normal
Di dalam dunia analisis data, pengetahuan tentang distribusi normal merupakan senjata berharga yang melengkapi para analis dalam menyelami kompleksitas data. Analisis data menggunakan distribusi normal menawarkan metodologi yang memungkinkan prediksi dan keputusan yang lebih bijak berdasarkan tren dan pola yang diidentifikasi.
Distribusi normal memungkinkan memahami data dengan lebih dalam, namun tantangan tetap ada dalam mengimplementasikannya secara efektif. Pemahaman dan fleksibilitas dalam menerapkan distribusi ini memastikan bahwa hasil analisis tetap relevan dan akurat meskipun dataset mengalami perkembangan. Dengan penguasaan distribusi normal, para analis dapat mengarahkan tim dan organisasi menuju sukses yang lebih besar, didorong oleh fondasi statistik yang solid.
Analisis data menggunakan distribusi normal tidak hanya tentang penerapan teknis, tetapi juga cara berpikir yang memperhatikan keberagaman dan karakter unik setiap data, serta cara paling efektif untuk menggali dan menginterpretasinya.