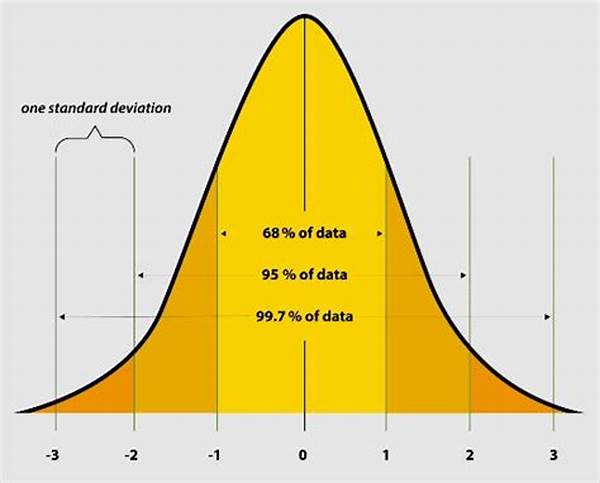
Dalam dunia statistik, distribusi normal menjadi sebuah konsep yang sangat penting dan mendasar. Keunikan dari distribusi ini adalah bentuknya yang simetris, dengan puncaknya berada di titik tengah. Namun, untuk bisa memanfaatkan distribusi normal ini dalam analisis statistik, kita memerlukan kemampuan untuk memprediksi atau mengestimasi parameter-parameter yang menyusunnya. Proses ini dikenal sebagai estimasi parameter distribusi normal. Dengan memahami cara memperkirakan parameter tersebut, kita bisa memberikan interpretasi yang lebih baik terhadap data yang kita miliki.
Mengapa Estimasi Parameter Distribusi Normal Dibutuhkan?
Dalam kegiatan penelitian atau analisis data, seringkali kita berhadapan dengan kumpulan data yang besar yang harus diinterpretasi. Untuk itu, kita memerlukan model yang tepat, dan distribusi normal sering kali menjadi pilihan. Namun, distribusi normal tersebut tidak bisa begitu saja diterapkan. Kita perlu mengidentifikasi dua parameter kuncinya: nilai rata-rata (mean) dan deviasi standar (standard deviation). Proses ini disebut sebagai estimasi parameter distribusi normal. Dengan estimasi ini, peluang untuk mendapatkan gambaran yang akurat dari data lebih besar. Kita dapat lebih percaya diri dalam menggunakan hasil analisis tersebut untuk membuat keputusan. Proses estimasi juga memberikan wawasan lebih dalam tentang bagaimana data didistribusikan, apakah data tersebut simetris, memiliki ekor panjang, atau bahkan mungkin terdistorsi.
Metode yang biasa digunakan untuk melakukan estimasi parameter distribusi normal adalah Metode Momen dan Maximum Likelihood Estimation (MLE). Kedua metode ini memberikan cara pandang yang berbeda dalam pendekatannya. Metode Momen, misalnya, menggunakan sifat-sifat momen dari distribusi untuk menentukan parameter. Sementara itu, MLE lebih memfokuskan pada menemukan nilai parameter yang membuat data yang kita miliki memiliki probabilitas tertinggi. Meskipun pendekatan yang diambil berbeda, keduanya bertujuan memberikan estimasi yang paling dekat dengan parameter sesungguhnya dari distribusi data.
Proses Estimasi Parameter Distribusi Normal
Dalam melakukan estimasi parameter distribusi normal, kita mulai dengan menghitung rata-rata dari dataset. Rata-rata ini menjadi indikasi pusat dari distribusi normal kita. Selanjutnya, kita menghitung deviasi standar, yang mencerminkan seberapa jauh individu data menyimpang dari rata-rata. Dengan kedua parameter ini, kita bisa membangun model distribusi normal yang paling representatif.
Tantangan dalam Estimasi Parameter Distribusi Normal
Meskipun terlihat sederhana, estimasi parameter distribusi normal menghadapi berbagai tantangan. Pertama, adanya outlier atau data yang menyimpang drastis dapat mengacaukan rata-rata dan deviasi standar. Kedua, ukuran sampel yang kecil bisa membuat estimasi menjadi kurang akurat. Oleh karena itu, penting melakukan pemilihan dan persiapan data dengan hati-hati agar estimasi memberikan hasil yang tepat.
1. Outlier Memengaruhi Estimasi: Kadang, data yang begitu ekstrem muncul dan menggeser rata-rata. Hal ini membuat estimasi parameter distribusi normal sulit diandalkan. Oleh karena itu, perlu dilakukan penanganan khusus terhadap outlier.
2. Ukuran Sampel: Semakin besar ukuran sampel, semakin kecil kesalahan dalam estimasi parameter. Ukuran sampel yang kecil akan mempengaruhi kualitas estimasi parameter distribusi normal.
3. Pemilihan Metode: Pemilihan metode estimasi, baik itu MLE atau Metode Momen, sangat bergantung pada karakteristik data. Pemahaman yang baik atas data adalah kunci.
4. Komputasi yang Kompleks: Proses estimasi terkadang menuntut perhitungan yang kompleks, terutama jika model distribusi yang dibangun cukup rumit.
5. Asumsi Distribusi Normal: Beberapa data gagal mengikuti asumsi distribusi normal. Hal ini tentu saja akan berdampak pada akurasi estimasi parameter distribusi normal.
Pengaruh Estimasi Parameter dalam Pengambilan Keputusan
Ketika parameter dari distribusi normal telah berhasil diestimasi, informasi tersebut dapat digunakan untuk berbagai analisis lanjut. Salah satu manfaat utamanya adalah penggunaan dalam pengambilan keputusan berbasis data. Misalnya, dalam bidang keuangan, estimasi parameter distribusi normal memungkinkan manajer investasi untuk menilai risiko dengan lebih akurat, sementara dalam bidang teknis, dapat membantu dalam kontrol kualitas produksi.
Dengan melakukan estimasi parameter distribusi normal, kita tak hanya dapat memodelkan data secara lebih akurat, tetapi juga mengidentifikasi potensi risiko yang mungkin terjadi. Parameter yang tepat juga memungkinkan kita untuk melakukan simulasi yang lebih mendekati kenyataan. Tidak hanya itu, banyak model statistik lanjutan yang menjadikan distribusi normal dan parameternya sebagai dasar utama. Oleh sebab itu, presentasi yang tepat dari distribusi ini memiliki dampak luas terhadap pendekatan analitis yang dilakukan.
Studi Kasus: Estimasi Parameter Distribusi Normal
Untuk memberikan gambaran nyata, bayangkan kita sedang mengerjakan sebuah proyek yang memerlukan analisis data berat badan remaja. Melalui beberapa metode seperti Metode Momen dan MLE, kita dapat menentukan estimasi parameter distribusi normal yakni rata-rata dan deviasi standar berat badan. Dengan informasi ini, kita bisa memahami pola distribusi berat badan dan melakukan prediksi yang lebih akurat mengenai tren kesehatan atau pengaruh pola makan terhadap berat badan.
Dalam studi kasus ini, kita belajar bahwa meskipun estimasi parameter distribusi normal sering kali dianggap remeh, proses ini sebenarnya memberikan banyak wawasan dalam berbagai aplikasi nyata. Proses estimasi tidak hanya menambah pemahaman kita mengenai data, tetapi juga memperkaya perspektif tentang bagaimana menangani data serupa di masa depan.
Kesimpulan Mengenai Estimasi Parameter Distribusi Normal
Seperti kisah perjalan yang telah kita lalui, estimasi parameter distribusi normal adalah sebuah perjalanan penting dalam statistik dan analisis data. Dengan memahami dan mengaplikasikan teknik estimasi parameter distribusi normal, kita dapat mengubah data mentah menjadi informasi berharga yang bisa mendukung pengambilan keputusan.
Perjalanan tidak selalu mulus, mengingat adanya tantangan dan hambatan, namun dengan persiapan dan pemahaman yang baik, estimasi parameter distribusi normal dapat diandalkan untuk memberikan gambaran distributif dari data yang kita analisis. Dan dari situlah, kita dapat terus melangkah, melampaui batasan, dan meraih hasil yang lebih baik dalam segala aspek penelitian maupun pekerjaan yang berkaitan dengan data statistik.